Under What Condition(S) On The Denominations Di Are You Able To Make Change For Any Amount M?

five.12. Dynamic Programming¶

Many programs in computer science are written to optimize some value; for example, discover the shortest path betwixt two points, find the line that all-time fits a set of points, or detect the smallest set of objects that satisfies some criteria. In that location are many strategies that computer scientists use to solve these bug. One of the goals of this book is to betrayal you to several different problem solving strategies. Dynamic programming is one strategy for these types of optimization issues.

A classic example of an optimization problem involves making modify using the fewest coins. Suppose you lot are a programmer for a vending machine manufacturer. Your company wants to streamline effort by giving out the fewest possible coins in change for each transaction. Suppose a client puts in a dollar bill and purchases an item for 37 cents. What is the smallest number of coins you tin can utilise to make change? The respond is six coins: two quarters, 1 dime, and three pennies. How did we arrive at the answer of vi coins? Nosotros start with the largest coin in our arsenal (a quarter) and use equally many of those as possible, then we go to the next lowest coin value and use equally many of those as possible. This offset approach is chosen a greedy method because we effort to solve as big a piece of the problem as possible right away.

The greedy method works fine when we are using U.Due south. coins, but suppose that your visitor decides to deploy its vending machines in Lower Elbonia where, in add-on to the usual one, five, 10, and 25 cent coins they also have a 21 cent coin. In this instance our greedy method fails to find the optimal solution for 63 cents in change. With the addition of the 21 cent money the greedy method would still find the solution to exist half dozen coins. However, the optimal answer is three 21 cent pieces.

Let'south look at a method where we could be certain that we would find the optimal answer to the problem. Since this section is about recursion, you may accept guessed that we will use a recursive solution. Let's offset with identifying the base case. If we are trying to make change for the same corporeality as the value of one of our coins, the reply is easy, one coin.

If the amount does non friction match we have several options. What nosotros want is the minimum of a penny plus the number of coins needed to make alter for the original amount minus a penny, or a nickel plus the number of coins needed to brand change for the original amount minus five cents, or a dime plus the number of coins needed to brand change for the original amount minus ten cents, then on. So the number of coins needed to make change for the original amount can be computed co-ordinate to the following:

\[\begin{dissever} numCoins = min \brainstorm{cases} 1 + numCoins(original amount - one) \\ 1 + numCoins(original corporeality - five) \\ 1 + numCoins(original amount - 10) \\ i + numCoins(original amount - 25) \end{cases} \characterization{eqn_change}\end{split}\]

The algorithm for doing what we have just described is shown in Listing seven. In line three nosotros are checking our base case; that is, we are trying to make change in the exact corporeality of ane of our coins. If we practise not have a coin equal to the corporeality of modify, nosotros brand recursive calls for each different money value less than the corporeality of alter we are trying to brand. Line 6 shows how we filter the list of coins to those less than the current value of change using a list comprehension. The recursive call besides reduces the total amount of modify we need to brand past the value of the coin selected. The recursive call is made in line vii. Notice that on that same line nosotros add 1 to our number of coins to account for the fact that we are using a coin. Just adding 1 is the aforementioned every bit if we had made a recursive call asking where nosotros satisfy the base case condition immediately.

Listing 7

1 2 3 four 5 6 7 8 9 10 xi 12

def recMC ( coinValueList , modify ): minCoins = modify if change in coinValueList : return i else : for i in [ c for c in coinValueList if c <= alter ]: numCoins = 1 + recMC ( coinValueList , change - i ) if numCoins < minCoins : minCoins = numCoins return minCoins print ( recMC ([ 1 , 5 , 10 , 25 ], 63 ))

The trouble with the algorithm in Listing vii is that it is extremely inefficient. In fact, information technology takes 67,716,925 recursive calls to discover the optimal solution to the 4 coins, 63 cents problem! To understand the fatal flaw in our approach look at Figure five, which illustrates a pocket-size fraction of the 377 function calls needed to find the optimal set of coins to make change for 26 cents.

Each node in the graph corresponds to a call to recMC . The label on the node indicates the amount of change for which nosotros are computing the number of coins. The label on the arrow indicates the coin that we but used. By following the graph we can meet the combination of coins that got u.s.a. to whatever point in the graph. The master problem is that nosotros are re-doing too many calculations. For instance, the graph shows that the algorithm would recalculate the optimal number of coins to make change for 15 cents at least three times. Each of these computations to find the optimal number of coins for 15 cents itself takes 52 role calls. Clearly we are wasting a lot of fourth dimension and endeavor recalculating erstwhile results.

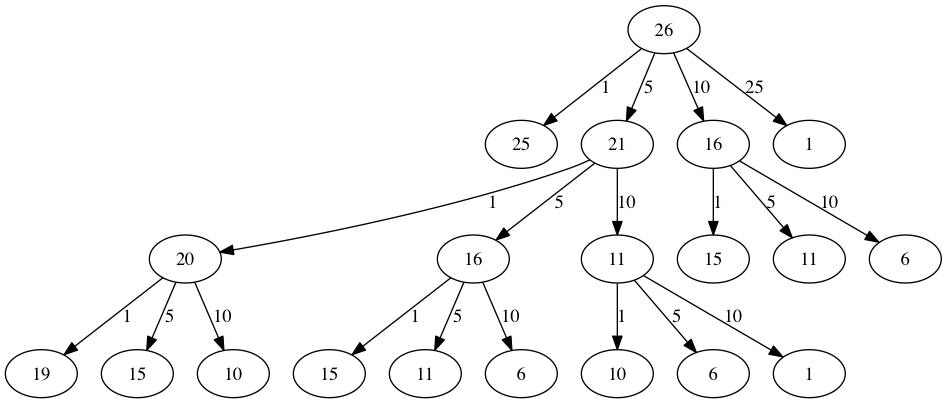
Figure iii: Call Tree for Listing seven¶

The key to cutting downwardly on the corporeality of work we do is to remember some of the by results and so nosotros can avoid recomputing results nosotros already know. A uncomplicated solution is to store the results for the minimum number of coins in a table when we find them. Then earlier we compute a new minimum, we starting time check the table to meet if a upshot is already known. If there is already a result in the table, nosotros utilise the value from the table rather than recomputing. ActiveCode 1 shows a modified algorithm to incorporate our table lookup scheme.

Notice that in line 6 we take added a test to see if our table contains the minimum number of coins for a certain amount of modify. If it does non, we compute the minimum recursively and shop the computed minimum in the tabular array. Using this modified algorithm reduces the number of recursive calls nosotros demand to brand for the four coin, 63 cent problem to 221 calls!

Although the algorithm in AcitveCode i is correct, information technology looks and feels similar a bit of a hack. Likewise, if we await at the knownResults lists we tin see that there are some holes in the tabular array. In fact the term for what we have done is not dynamic programming but rather nosotros have improved the functioning of our program by using a technique known as "memoization," or more commonly chosen "caching."

A truly dynamic programming algorithm will take a more systematic arroyo to the problem. Our dynamic programming solution is going to start with making change for one cent and systematically work its mode upwardly to the amount of change we require. This guarantees u.s.a. that at each step of the algorithm we already know the minimum number of coins needed to brand change for any smaller amount.

Allow'due south look at how we would fill in a tabular array of minimum coins to use in making change for 11 cents. Figure four illustrates the process. We get-go with 1 cent. The merely solution possible is 1 coin (a penny). The next row shows the minimum for one cent and two cents. Over again, the only solution is two pennies. The fifth row is where things go interesting. At present we accept two options to consider, 5 pennies or one nickel. How practice we decide which is all-time? Nosotros consult the table and come across that the number of coins needed to make change for four cents is iv, plus one more than penny to make five, equals five coins. Or we can expect at aught cents plus ane more nickel to make five cents equals 1 coin. Since the minimum of one and five is one nosotros store one in the tabular array. Fast forward once again to the end of the table and consider 11 cents. Effigy 5 shows the three options that nosotros have to consider:

1. A penny plus the minimum number of coins to make change for \(11-1 = x\) cents (i)

2. A nickel plus the minimum number of coins to brand change for \(11 - 5 = 6\) cents (ii)

3. A dime plus the minimum number of coins to make modify for \(11 - 10 = one\) cent (1)

Either option 1 or three will requite us a total of two coins which is the minimum number of coins for 11 cents.

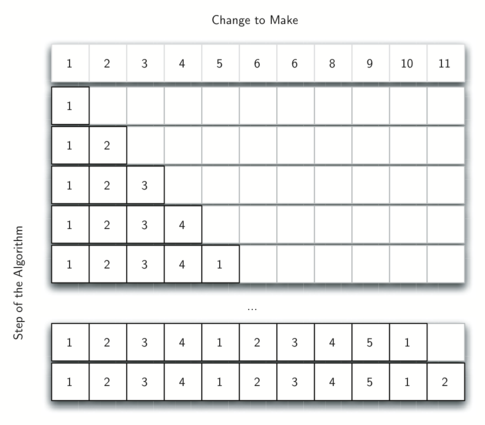
Effigy 4: Minimum Number of Coins Needed to Make Modify¶

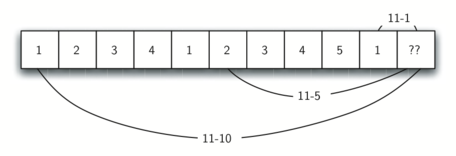
Figure 5: Three Options to Consider for the Minimum Number of Coins for 11 Cents¶

Listing 8 is a dynamic programming algorithm to solve our modify-making problem. dpMakeChange takes three parameters: a list of valid money values, the amount of alter nosotros want to make, and a list of the minimum number of coins needed to make each value. When the function is done minCoins volition comprise the solution for all values from 0 to the value of change .

Listing 8

                        def            dpMakeChange            (            coinValueList            ,            change            ,            minCoins            ):            for            cents            in            range            (            change            +            1            ):            coinCount            =            cents            for            j            in            [            c            for            c            in            coinValueList            if            c            <=            cents            ]:            if            minCoins            [            cents            -            j            ]            +            i            <            coinCount            :            coinCount            =            minCoins            [            cents            -            j            ]            +            i            minCoins            [            cents            ]            =            coinCount            return            minCoins            [            modify            ]          

Note that dpMakeChange is not a recursive function, even though we started with a recursive solution to this problem. It is of import to realize that just because you can write a recursive solution to a problem does non mean it is the best or near efficient solution. The bulk of the work in this function is done by the loop that starts on line 4. In this loop nosotros consider using all possible coins to make modify for the corporeality specified past cents . Similar we did for the 11 cent case above, we recall the minimum value and store information technology in our minCoins list.

Although our making change algorithm does a good chore of figuring out the minimum number of coins, it does not assist usa make change since we exercise not go on rails of the coins we use. We can easily extend dpMakeChange to keep track of the coins used by simply remembering the concluding coin we add for each entry in the minCoins table. If we know the last coin added, we can only subtract the value of the coin to find a previous entry in the table that tells us the concluding money nosotros added to make that corporeality. We can continue tracing back through the table until nosotros become to the beginning.

ActiveCode two shows the dpMakeChange algorithm modified to keep runway of the coins used, along with a role printCoins that walks backward through the table to print out the value of each coin used. This shows the algorithm in activeness solving the problem for our friends in Lower Elbonia. The first 2 lines of primary set the amount to exist converted and create the list of coins used. The next two lines create the lists we need to store the results. coinsUsed is a list of the coins used to brand change, and coinCount is the minimum number of coins used to brand change for the amount respective to the position in the listing.

Observe that the coins we print out come directly from the coinsUsed array. For the showtime call we outset at array position 63 and print 21. And so we take \(63 - 21 = 42\) and look at the 42nd element of the list. Once once again we find a 21 stored there. Finally, element 21 of the assortment also contains 21, giving u.s.a. the three 21 cent pieces.

Source: https://runestone.academy/ns/books/published/pythonds/Recursion/DynamicProgramming.html

Posted by: michaelquithethand.blogspot.com

Share this post